Talk:Abaddon charm: Difference between revisions
No edit summary |
SIGN. COMMENTS. ESPECIALLY. |
||
| Line 102: | Line 102: | ||
I think there is a significance to the fact that getting a hash number of 1 or of 36 is 1 to 666 (approx.). This being the abaddon charm and the pit and all. Can't overlook 666. | I think there is a significance to the fact that getting a hash number of 1 or of 36 is 1 to 666 (approx.). This being the abaddon charm and the pit and all. Can't overlook 666. | ||
I just wanted to pop in to tell you to sign your comments...ESPECIALLY if you haven't registered an account. --[[User:MagiNinjA|User:MagiNinjA/sig]] 11:29, 5 January 2008 (MST) | |||
Revision as of 18:29, 5 January 2008
"Therum has been quoted saying "It's rather simple, but it's also genius. And that's all I'll say."" ... um... what? Cristiona 21:25, 15 December 2007 (MST)
- Oh, I get it. Each fiend has three adjectives, and each (first, second, third) adjective is taken from a table of adjectives. Each possible fiend's name can be described by three numbers, one for each table. How much you wanna bet the adjectives on the tables are in alphabetical order? Last hint: 1A 2B 3C 4D 5E ... 25Y 26Z. --Mozai 15:18, 18 December 2007 (MST)
- If I'm right, the chances of fighting the correct fiend should be 1 in 729... maybe 1 in 6561. -Mozai 15:22, 18 December 2007 (MST)
All 4 name parts are used as indexes. Their indexes are not in alphabetical order. - Satan
Since Ryme is a programmer, the drop is probably determined by a simple hash table calculation and here is how it probably works. The program randomly selects an integer from 1 to 9; it does this four times to get each part of the monster name from the four lists. Then the four index values are added to get a hash sum, which in this case must fall in the range from 4 (all ones) to 36 (all nines). Any combination of index numbers that sums to the desired hash value should drop the talisman.
Depending on the winning hash value Ryme selected, the probability of the drop could be anywhere from low of 0.015% to a high of 7.453% (he could also have programmed multiple winning values such as 4 OR 36). Given the rarity of this item, the target value(s) is obviously one of the low frequency choices near the top or bottom of the table shown below. For example, if the target hash sum is 5, there are four monster name combinations (out of 6,561 possibilities) that will drop the talisman, while if the value is 6 there are ten combinations, etc.
Unfortunately, knowing the programming technique is just interesting information; that knowledge does not help you get an Abaddon Charm any sooner! If you want the talisman, you have to go to the pit, kill some monsters, and get lucky. - Hodag
| Hash | Frequency | Probability | |
|---|---|---|---|
| 4 | 1 | 0.015% | |
| 5 | 4 | 0.061% | |
| 6 | 10 | 0.152% | |
| 7 | 20 | 0.305% | |
| 8 | 35 | 0.533% | |
| 9 | 56 | 0.854% | |
| 10 | 84 | 1.280% | |
| 11 | 120 | 1.829% | |
| 12 | 165 | 2.515% | |
| 13 | 216 | 3.292% | |
| 14 | 270 | 4.115% | |
| 15 | 324 | 4.938% | |
| 16 | 375 | 5.716% | |
| 17 | 420 | 6.401% | |
| 18 | 456 | 6.950% | |
| 19 | 480 | 7.316% | |
| 20 | 489 | 7.453% | |
| 21 | 480 | 7.316% | |
| 22 | 456 | 6.950% | |
| 23 | 420 | 6.401% | |
| 24 | 375 | 5.716% | |
| 25 | 324 | 4.938% | |
| 26 | 270 | 4.115% | |
| 27 | 216 | 3.292% | |
| 28 | 165 | 2.515% | |
| 29 | 120 | 1.829% | |
| 30 | 84 | 1.280% | |
| 31 | 56 | 0.854% | |
| 32 | 35 | 0.533% | |
| 33 | 20 | 0.305% | |
| 34 | 10 | 0.152% | |
| 35 | 4 | 0.061% | |
| 36 | 1 | 0.015% | |
| Total | 6,561 | 100.000% |
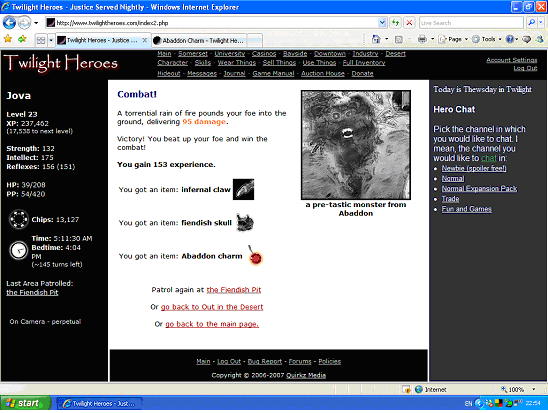
02 Jan 2008, 22:50 (GMT) -- Jova acquires Abaddon Charm from creature called "a pre-tastic monster from Abaddon". Hope this helps anyone out there :) -- Jova.
You got a screen shot of that? Verification, you see. All previous charms (quite a few) have come from Freak-tesque fiends from the inferno. - Satan
This is the pit fiend I found which dropped the Abaddon charm. -- Jova
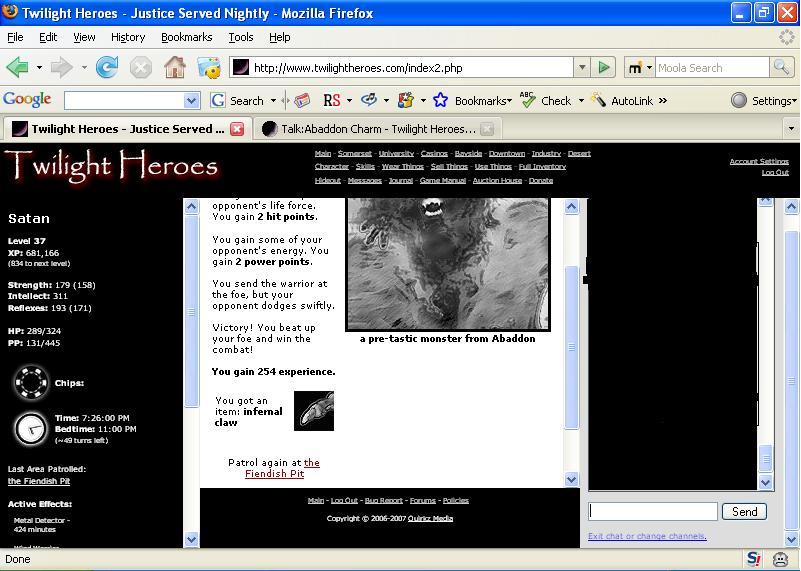
Hrm. I got this today.
Although the hash numbers seem a definite likelihood, I was wondering if either real-life time or game time would come into the equation as well? It seems odd that pit fiends with the same names would give different odds of item drops, or different item drops altogether, so perhaps there is another factor which we're missing? -- Jova.
I think there is a significance to the fact that getting a hash number of 1 or of 36 is 1 to 666 (approx.). This being the abaddon charm and the pit and all. Can't overlook 666.
I just wanted to pop in to tell you to sign your comments...ESPECIALLY if you haven't registered an account. --User:MagiNinjA/sig 11:29, 5 January 2008 (MST)